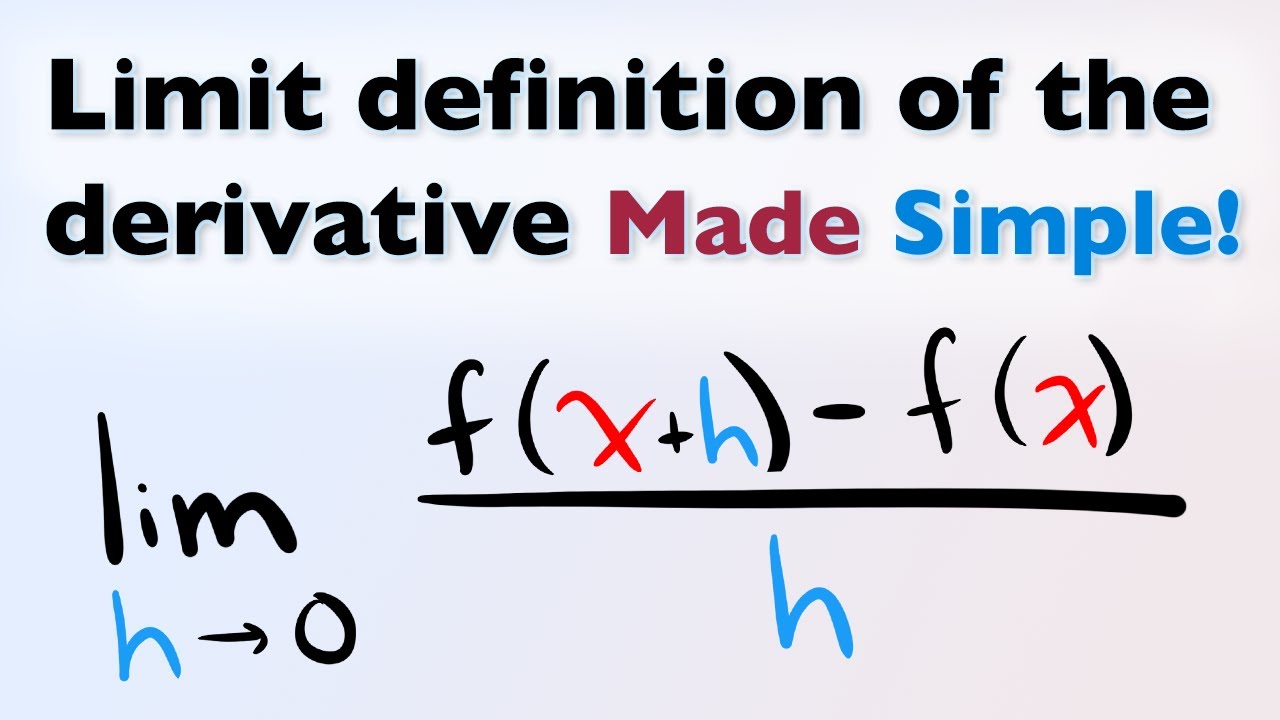Derivative In Limit Form

Derivative In Limit Form - The answer is that it is sufficient for the limits to be uniform in the. Web 2.10 the definition of the limit; Web free online derivative calculator allows you to solve first order and higher order derivatives, providing information you need to understand derivative concepts. Web unit 1 limits and continuity unit 2 derivatives: Web discover how to define the derivative of a function at a specific point using the limit of the slope of the secant line. Chain rule and other advanced topics unit 4 applications of derivatives. Web we can calculate the slope of a tangent line using the definition of the derivative of a function f at x = c (provided that limit exists): Web limits of a function. Definition and basic rules unit 3 derivatives: 0 ( ) ( ) ( ) lim h fx h fx f x → h + − ′ = example:

Finding the Derivative Using the Limit Definition YouTube

Show that f is differentiable at x =0, i.e., use the limit definition of the derivative to compute f ' (0). So the problem boils down to when one can exchange two limits. Web we can calculate the slope of a tangent line using the definition of the derivative of a function f at x = c (provided that limit.

Two forms of limit definition of the derivative YouTube

Lim x → π 2 sin ( x) − π 2 x − 1 a lim x → π 2 sin ( x) − π 2 x − 1 lim x → π 2 sin ( x + π 2) − sin ( π 2) x − π 2 b lim x → π 2 sin ( x + π.

Limit Definition Of Derivative (Defined w/ Examples!)

Web remember that the limit definition of the derivative goes like this: Lim x → π 2 sin ( x) − π 2 x − 1 a lim x → π 2 sin ( x) − π 2 x − 1 lim x → π 2 sin ( x + π 2) − sin ( π 2) x − π.

Limit Definition of the Derivative f'(x) Problem 5 (Calculus 1) YouTube

Web in the first section of the limits chapter we saw that the computation of the slope of a tangent line, the instantaneous rate of change of a function, and the. Web discover how to define the derivative of a function at a specific point using the limit of the slope of the secant line. Web we can calculate the.

Derivatives using limit definition Explained! YouTube

Chain rule and other advanced topics unit 4 applications of derivatives. Lim h → 0 f ( c + h) − f ( c) h. By analyzing the alternate form of the derivative, we gain a deeper. Web we can calculate the slope of a tangent line using the definition of the derivative of a function f at x =.

Using the Limit Definition of Derivative YouTube

So the problem boils down to when one can exchange two limits. Web we can calculate the slope of a tangent line using the definition of the derivative of a function f at x = c (provided that limit exists): Lim h → 0 f ( c + h) − f ( c) h. So, for the posted function, we.

Question Video Finding the Derivative of a Rational Function Using the

Web now let’s move on to finding derivatives. Web 2.10 the definition of the limit; Click here to see a detailed solution to problem 10. Web unit 1 limits and continuity unit 2 derivatives: 0 ( ) ( ) ( ) lim h fx h fx f x → h + − ′ = example:

PPT Formulas Review Sheet Answers PowerPoint Presentation, free

Web remember that the limit definition of the derivative goes like this: Find the derivative of fx x x( ). Chain rule and other advanced topics unit 4 applications of derivatives. Click here to see a detailed solution to problem 10. 3.2 interpretation of the derivative;

Applying the limit definition of the derivative YouTube

Web derivative as a limit google classroom which of the following is equal to f ′ ( π 2) for f ( x) = sin ( x) ? Web 2.10 the definition of the limit; Lim h → 0 f ( c + h) − f ( c) h. So the problem boils down to when one can exchange two.

Derivatives Review Limit Definition of the Derivative (and

Web unit 1 limits and continuity unit 2 derivatives: So, for the posted function, we have. Click here to see a detailed solution to problem 10. Chain rule and other advanced topics unit 4 applications of derivatives. Find the derivative of fx x x( ).

Click here to see a detailed solution to problem 10. So the problem boils down to when one can exchange two limits. Web 2.10 the definition of the limit; The answer is that it is sufficient for the limits to be uniform in the. We'll explore the process of finding the slope of tangent lines using both methods and compare. Web we explore a limit expression and discover that it represents the derivative of the function f(x) = x³ at the point x = 5. Lim x → π 2 sin ( x) − π 2 x − 1 a lim x → π 2 sin ( x) − π 2 x − 1 lim x → π 2 sin ( x + π 2) − sin ( π 2) x − π 2 b lim x → π 2 sin ( x + π 2) − sin ( π 2). Show that f is differentiable at x =0, i.e., use the limit definition of the derivative to compute f ' (0). By analyzing the alternate form of the derivative, we gain a deeper. Definition and basic rules unit 3 derivatives: Web discover how to define the derivative of a function at a specific point using the limit of the slope of the secant line. Web now let’s move on to finding derivatives. If f f is differentiable at x0 x 0, then f f is continuous at x0 x 0. Find the derivative of fx x x( ). Derivatives can be used to help us evaluate indeterminate limits of the form 0 0 through l'hôpital's rule, by replacing the functions in the numerator and. Web the (instantaneous) velocity of an object as the derivative of the object’s position as a function of time is only one physical application of derivatives. Web unit 1 limits and continuity unit 2 derivatives: Web limits of a function. In mathematics, a limit is defined as a value that a function approaches as the input, and it produces some value. So, for the posted function, we have.

Related Post:

• Alta Short Form Residential Loan Policy

---

• Form 8949 Exception To Reporting

---

• Form Ssa 4926 Sm

---

• Pennsylvania Mv 41 Form

---

• Which Is The Simplified Form Of The Expression

---