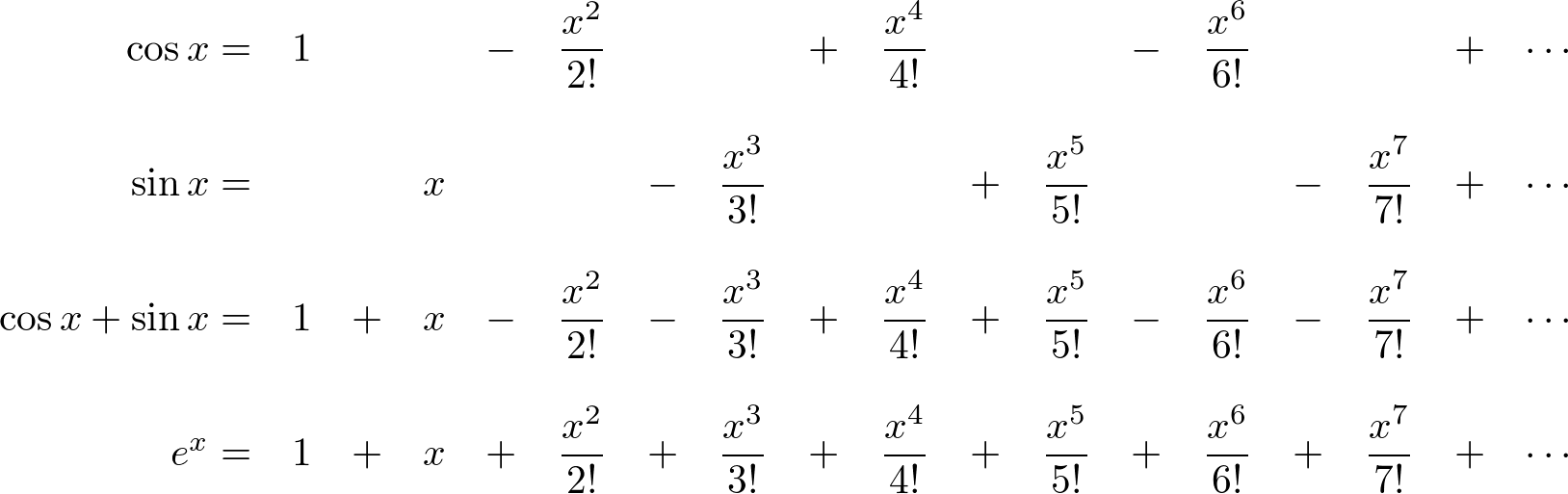Sinx In Exponential Form
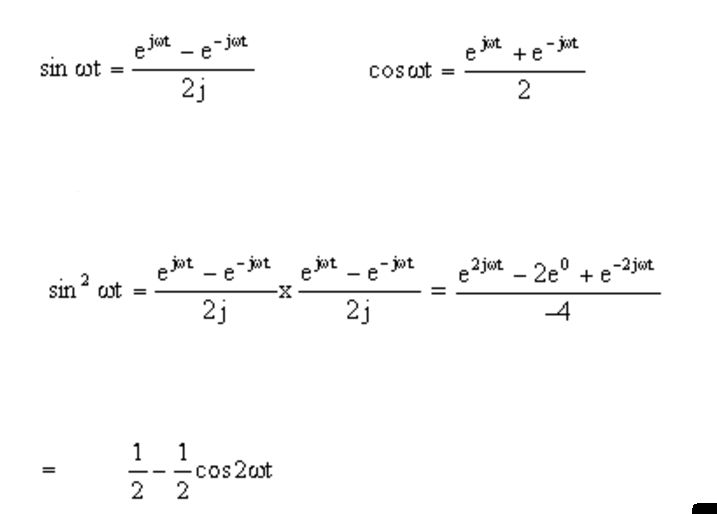
Sinx In Exponential Form - E x = ∑ n = 0 ∞ x n n! Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Eix = ∑∞ n=0 (ix)n n! 16 + 2 / 3 g: Web \the complex exponential function is periodic with period 2…i. the flrst thing we want to show in these notes is that the period 2…i is \minimal in the same sense that 2… is the. 0.2588 + 0.9659 30° 1 / 6 π: (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Suppose i have a complex variable j j such that we have. What is going on, is that electrical engineers tend to ignore the fact that one needs to add or subtract the complex. Could somebody please explain how this turns into a sinc. Web \the complex exponential function is periodic with period 2…i. the flrst thing we want to show in these notes is that the period 2…i is \minimal in the same sense that 2… is the. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the. Web property of the exponential, now extended to any complex numbers c 1 = a 1+ib 1 and c 2 = a 2 + ib 2, giving ec 1+c 2 =ea 1+a 2ei(b 1+b 2) =ea 1+a 2(cos(b 1 + b 2) + isin(b 1 + b. The exponent calculator simplifies the given exponential expression using the laws of exponents.. Web \the complex exponential function is periodic with period 2…i. the flrst thing we want to show in these notes is that the period 2…i is \minimal in the same sense that 2… is the. Web we can work out tanhx out in terms of exponential functions. This formula can be interpreted as saying that the function e is a. Web sin(x) cos(x) degrees radians gradians turns exact decimal exact decimal 0° 0 0 g: Z (eat cos bt+ieat sin bt)dt = z e(a+ib)t dt = 1 a+ib e(a+ib)t +c = a¡ib a2 +b2 (eat cos bt+ieat sin bt)+c = a a2 +b2 eat. Web simultaneously, integrate the complex exponential instead! Web we can work out tanhx out in terms. I like to write series with a summation sign rather than individual terms. Enter an exponential expression below which you want to simplify. Sin z = exp(iz) − exp(−iz) 2i sin z = exp ( i z) − exp ( − i z) 2 i. Web sin(x) cos(x) degrees radians gradians turns exact decimal exact decimal 0° 0 0 g:. Eix = ∑∞ n=0 (ix)n n! E^x = sum_(n=0)^oo x^n/(n!) so: 33 + 1 / 3 g: The exponent calculator simplifies the given exponential expression using the laws of exponents. Web this is very surprising. From the definitions we have. Suppose i have a complex variable j j such that we have. Web simultaneously, integrate the complex exponential instead! E x = ∑ n = 0 ∞ x n n! I like to write series with a summation sign rather than individual terms. So adding these two equations and dividing. In order to easily obtain trig identities like , let's write and as complex exponentials. Z denotes the exponential function. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. From the definitions we have. Web we can work out tanhx out in terms of exponential functions. Rewriting 𝑒 = 𝑒, ( ) we can apply euler’s formula to get 𝑒 = ( − 𝜃) + 𝑖 ( − 𝜃). In this case, ex =∑∞ n=0 xn n! E^x = sum_(n=0)^oo x^n/(n!) so: Suppose i have a complex variable j j such that we have. Web sin(x) cos(x) degrees radians gradians turns exact decimal exact decimal 0° 0 0 g: Web this, of course, uses three interconnected formulas: E^x = sum_(n=0)^oo x^n/(n!) so: 0.2588 + 0.9659 30° 1 / 6 π: The exponent calculator simplifies the given exponential expression using the laws of exponents. So adding these two equations and dividing. Web relations between cosine, sine and exponential functions. The exponent calculator simplifies the given exponential expression using the laws of exponents. What is going on, is that electrical engineers tend to ignore the fact that one needs to add or subtract the complex. In this case, ex =∑∞ n=0 xn n! Web \the complex exponential function is periodic with period 2…i. the flrst thing we want to show in these notes is that the period 2…i is \minimal in the same sense that 2… is the. 0 0 0 1 1 15° 1 / 12 π: Web we can work out tanhx out in terms of exponential functions. For any complex number z z : E^(ix) = sum_(n=0)^oo (ix)^n/(n!) = sum_(n. Web simultaneously, integrate the complex exponential instead! Sin z = exp(iz) − exp(−iz) 2i sin z = exp ( i z) − exp ( − i z) 2 i. Web this is very surprising. E^x = sum_(n=0)^oo x^n/(n!) so: This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Enter an exponential expression below which you want to simplify. Could somebody please explain how this turns into a sinc. Web property of the exponential, now extended to any complex numbers c 1 = a 1+ib 1 and c 2 = a 2 + ib 2, giving ec 1+c 2 =ea 1+a 2ei(b 1+b 2) =ea 1+a 2(cos(b 1 + b 2) + isin(b 1 + b. In order to easily obtain trig identities like , let's write and as complex exponentials.Example 5 Express tan1 cosx/(1 sinx) Chapter 2 Inverse
Function For Sine Wave Between Two Exponential Cuves Mathematics
Basics of QPSK modulation and display of QPSK signals Electrical
Complex Numbers 4/4 Cos and Sine to Complex Exponential YouTube
Euler's Equation
Solved 5. Euler's equations are defined as sin (x) cos(x) e"
y= e^√(2 sinx); find dy/dx Exponential & Trigonometric function
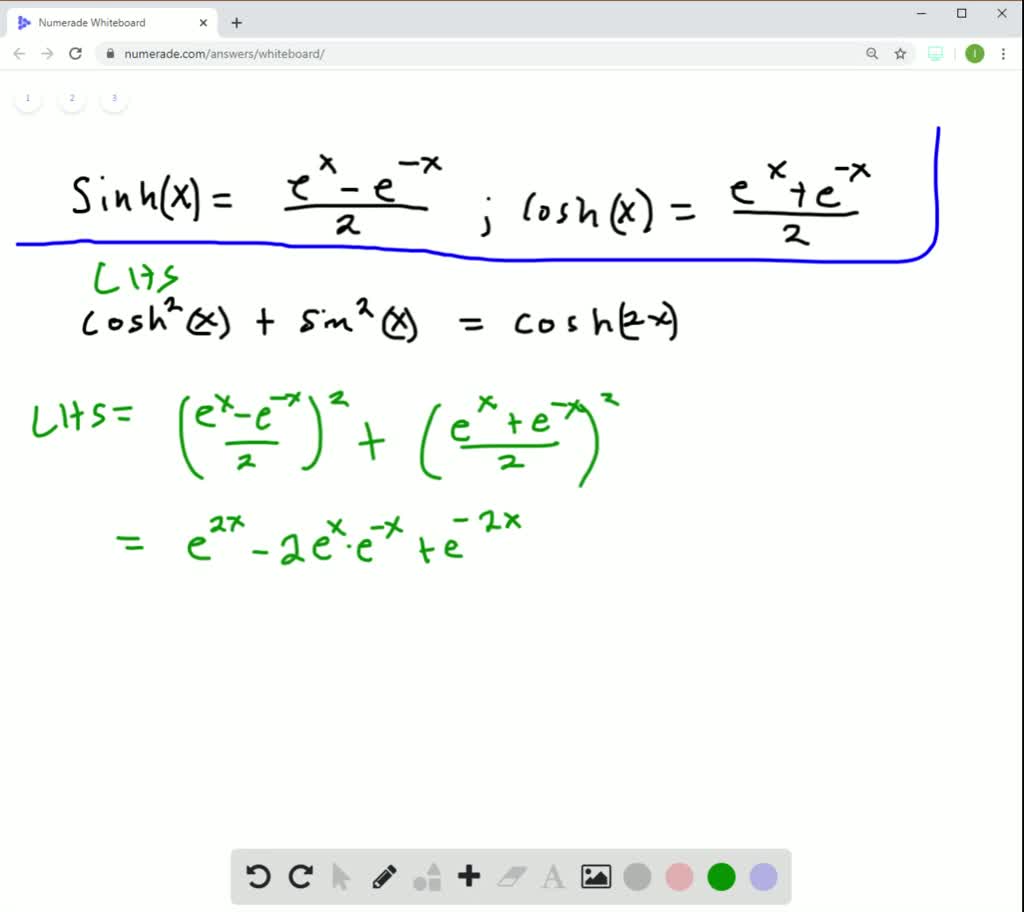
SOLVEDExpress \cosh 2 x and \sinh 2 x in exponential form and hence
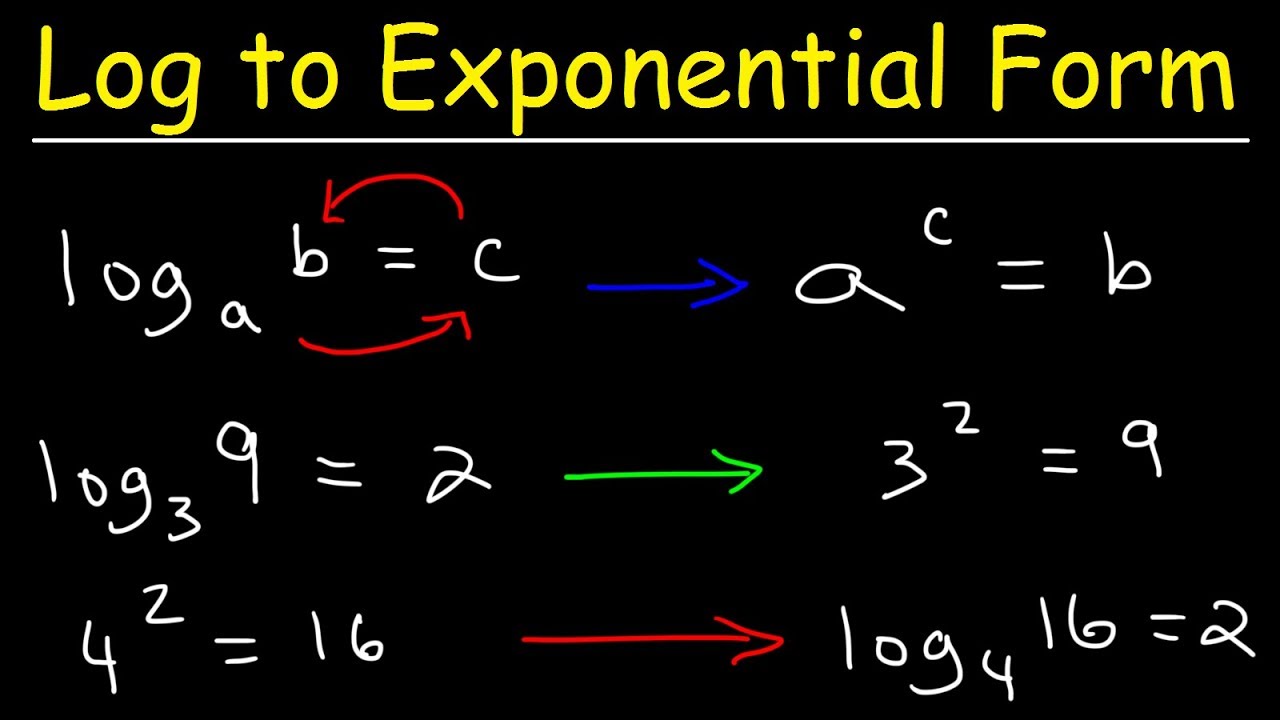
Writing Logarithmic Equations In Exponential Form YouTube
How to write expressions in exponential form
Related Post: