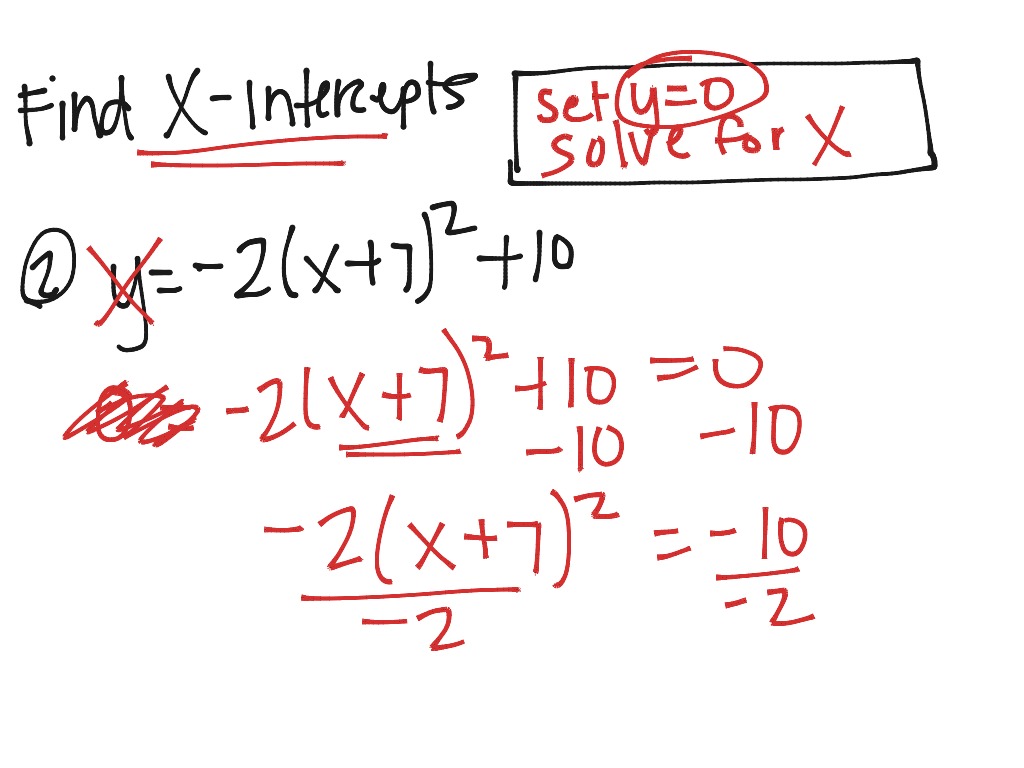Y Intercept From Vertex Form

Y Intercept From Vertex Form - Web the transformation can be a vertical/horizontal shift, a stretch/compression or a refection. 𝑦 = 𝑎 (𝑥² + (𝑏 ∕ 𝑎)𝑥) + 𝑐 = = 𝑎 (𝑥 + 𝑏 ∕ (2𝑎))² + 𝑐 − 𝑏² ∕ (4𝑎) with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) we get. Y = 2 x 2 + 24 x + 59. If a is positive, the parabola opens up. Look at the coefficient of the x^2 term. 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐 for 𝑎 ≠ 0. It is the constant term. By factoring out 𝑎 and completing the square, we get. Add and subtract (b/(2a))² inside the bracket: Vertex form is best for finding the vertex of the.

ShowMe find y intercept from a table

Y = a[x² + (b/a)x] + c. You can also convert the standard form to vertex form through this calculator. Standard form of given equation is: A parabola is defined as. If a is negative, then the parabola opens down.

X intercept vertex form Math ShowMe

Factored form looks like this: 𝑦 = 𝑎 (𝑥² + (𝑏 ∕ 𝑎)𝑥) + 𝑐 = = 𝑎 (𝑥 + 𝑏 ∕ (2𝑎))² + 𝑐 − 𝑏² ∕ (4𝑎) with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) we get. Y = a (x + b)2 + c where a, b and c are known.

How to Learn and Solve for xintercepts using Vertex Form Grade 11

You can also convert the standard form to vertex form through this calculator. Add and subtract (b/(2a))² inside the bracket: It is the constant term. Given a quadratic equation in the vertex form i.e. Extract a from the first two terms:

Using Vertex Form to Solve for Xintercepts YouTube

Y = 2 x 2 + 24 x + 59. If a is positive, the parabola opens up. The sign of a determines the direction of the parabola. Web to convert the standard form y = ax² + bx + c to vertex form: You can also convert the standard form to vertex form through this calculator.

How to Solve X Intercepts from Vertex Form Grade 10 Academic Lesson 6 5

Add and subtract (b/(2a))² inside the bracket: If a is positive, the parabola opens up. Web for standard form: Web the transformation can be a vertical/horizontal shift, a stretch/compression or a refection. A parabola is defined as.

Finding X Intercepts of Quadratics from Vertex Form Grade 11 Mixed

Y = a (x + b)2 + c where a, b and c are known constants and x and y are variables. Y = a[x² + (b/a)x] + c. By factoring out 𝑎 and completing the square, we get. Add and subtract (b/(2a))² inside the bracket: Factored form looks like this:

Find Y Intercept Given Vertex and X Intercept YouTube

Y = a[x² + (b/a)x] + c. Add and subtract (b/(2a))² inside the bracket: A parabola is defined as. 𝑦 = 𝑎 (𝑥² + (𝑏 ∕ 𝑎)𝑥) + 𝑐 = = 𝑎 (𝑥 + 𝑏 ∕ (2𝑎))² + 𝑐 − 𝑏² ∕ (4𝑎) with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) we get. Given.

How To Find X Intercepts Of A Parabola X = −b ± √b2 −4ac 2a

Web 6 years ago. Standard form of given equation is: By factoring out 𝑎 and completing the square, we get. Factored form looks like this: If a is positive, the parabola opens up.

PPT Converting Quadratic Equations PowerPoint Presentation, free

Web for standard form: If a is negative, then the parabola opens down. If a is positive, the parabola opens up. 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐 for 𝑎 ≠ 0. The sign of a determines the direction of the parabola.

XIntercepts From Vertex Form of a Quadratic Equation YouTube

You can also convert the standard form to vertex form through this calculator. Look at the coefficient of the x^2 term. Web 6 years ago. How to use vertex form. If a is positive, the parabola opens up.

𝑦 = 𝑎 (𝑥² + (𝑏 ∕ 𝑎)𝑥) + 𝑐 = = 𝑎 (𝑥 + 𝑏 ∕ (2𝑎))² + 𝑐 − 𝑏² ∕ (4𝑎) with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) we get. Web the transformation can be a vertical/horizontal shift, a stretch/compression or a refection. The sign of a determines the direction of the parabola. Y = a[x² + (b/a)x] + c. If a is positive, the parabola opens up. Web for standard form: Web to convert the standard form y = ax² + bx + c to vertex form: It is also the point at which. 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐 for 𝑎 ≠ 0. It is the constant term. Standard form of given equation is: By factoring out 𝑎 and completing the square, we get. Y = a (x + r1) (x + r2). Add and subtract (b/(2a))² inside the bracket: If a is negative, then the parabola opens down. Extract a from the first two terms: Given a quadratic equation in the vertex form i.e. How to use vertex form. Identifying the characteristics of a parabola. Vertex form is best for finding the vertex of the.

Related Post:

• Final Form Gif

---

• Keldeo Resolute Form Pokemon Go

---

• Form 433 A Fillable

---

• Childe Foul Legacy Form

---

• Iowa Representative Certification Form

---