How To Write Vectors In Component Form
How To Write Vectors In Component Form - A vector whose initial point is the origin so its coordinates are (0,0) and its terminal point has coordinates (v1,v2 ( v 1, v 2 then the. Y z x y z x p o 3 6 4. Therefore, we can find each component using the cos (for the x component) and sin (for the y component) functions: Web the component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down a vector is going. Remember that component form is the form < x, y > and to translate from magnitude r and direction θ to component form, use the relationship < r. Web 8 years ago remember, in a vector, there is a specific beginning and ending point, and the ending point is marked as an arrow. Web introduction to vector components google classroom about transcript vectors are quantities that have a magnitude and a direction. Web one advantage of rewriting the vectors in component form is that much of this work is simplified. 2 ) = (1, 3) = 〈0, 6〉 subtract. Web when separating a vector into its component form, we are essentially creating a right triangle with the vector being the hypotenuse. Web a vector is defined as a quantity with both magnitude and direction. The reason an arrow is used is because a vector uses magnitude, the amount something moves, or the speed with which it moves, and direction. Write the component form of the vector as v. A vector o p → is shown below. Web in component form, we. G (g 1, g 2) Identify the initial and terminal points of the vector. The component form of a vector →v is written as →v= vx,vy v → = v x , v y , where vx represents the horizontal displacement between the initial and terminal points, and vy represents the vertical displacement between the initial and terminal points. Component. Round your final answers to the nearest hundredth. Web express a vector in component form. The components of a vector gives a split of the vector. The magnitude of a vector is the length of the vector. 2 ) = (1, 3) = 〈0, 6〉 subtract. Web express a vector in component form. Web the component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down a vector is going. The vector is split with reference to each of the axes, and we can compute. The components of a vector gives a split of the vector. Web introduction to vector components google classroom about transcript vectors are quantities that have a magnitude and a direction. Y x 8 300 ∘ find the component form of u →. 2 ) = (1, 3) = 〈0, 6〉 subtract. This representative of vector v is in standard position. Web learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in component form. I ^ + j ^ + k ^. H (h 1, h 2) gh−⇀− = h1 −g1,h2 −g2 = u1,u2 =u g h ⇀ = 〈 h 1 − g 1, h 2. A vector whose initial point is the origin so its coordinates are (0,0) and its terminal point has coordinates (v1,v2 ( v 1, v 2 then the. Web learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in component form. Write the component form of the. Y x 8 300 ∘ find the component form of u →. Remember that component form is the form < x, y > and to translate from magnitude r and direction θ to component form, use the relationship < r. Web 8 years ago remember, in a vector, there is a specific beginning and ending point, and the ending point. Y z x y z x p o 3 6 4. Web to find the components of a vector from its magnitude and direction, we multiply the magnitude by the sine or cosine of the angle: Learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in.. In this article, we'll cover what vectors are, different ways to write them, and the three basic vector operations. Web a vector is defined as a quantity with both magnitude and direction. Web learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in component form. 2. Web vectors are the building blocks of everything multivariable. A vector o p → is shown below. Web what are the components of a vector? How do you draw a vector in component form? Web express a vector in component form. The component form of a vector →v is written as →v= vx,vy v → = v x , v y , where vx represents the horizontal displacement between the initial and terminal points, and vy represents the vertical displacement between the initial and terminal points. U → ≈ ( , ). The vector is split with reference to each of the axes, and we can compute the components of a vector. Identify the initial and terminal points of the vector. Given a vector’s initial point (where it starts), (x₁, y₁), and terminal point (where it ends), (x₂, y₂) the component form can be found by subtracting the coordinates of. The individual components of a vector can be later combined to get the entire vector representation. Hsn.vm.b.4.b google classroom you might need: G (g 1, g 2) terminal point: Web one advantage of rewriting the vectors in component form is that much of this work is simplified. Remember that component form is the form < x, y > and to translate from magnitude r and direction θ to component form, use the relationship < r. The magnitude of a vector is the length of the vector. Therefore, we can find each component using the cos (for the x component) and sin (for the y component) functions: Component form of directed line segment: Web the component form of vector ab with a(a x, a y) and b(b x, b y) can be found using the following formula: Find the horizontal displacement v x = x 2 − x 1, where x 2 is the x − coordinate of the terminal point and x 1.How to write a vector in components YouTube
Component Vectors CK12 Foundation
Vectors Component form and Addition YouTube
Pc 6.3 notes_vectors
Vectors 2a Component Form YouTube
PC 6.3 Notes Example 8 Find the Component Form of a Vector YouTube
Question Video Writing a Vector in Component Form Nagwa
Question Video Calculating the Sum of Two Vectors in Component Form
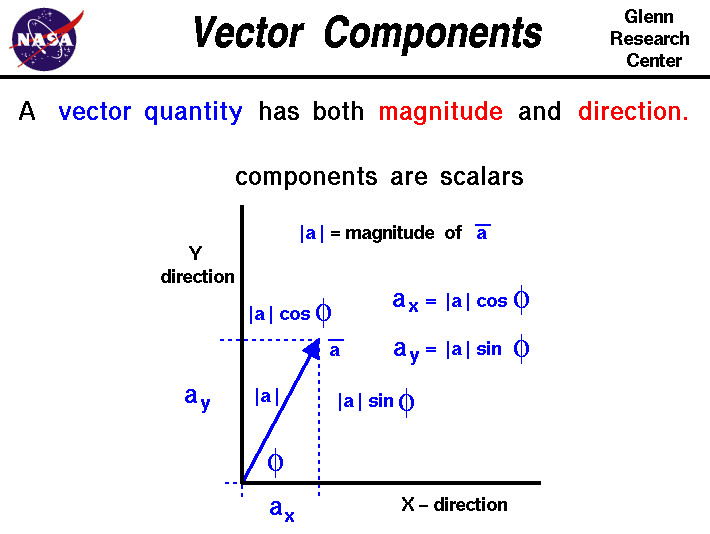
Vector Components
Component Form of Vectors YouTube
Related Post: