Express The Given Hindu Arabic Numeral In Expanded Form
Express The Given Hindu Arabic Numeral In Expanded Form - Do not perform the calculation.). (7 × 103) + (5 × 101) + (4 × 1). 5,000 + 300 + 20 + 5 = 5,325 expanded factors form: ( 9 × 1 0 1 ) + ( 4 × 1 ) \left(9 \times 10^{1}\right)+(4 \times 1) ( 9 × 1 0 1 ) + ( 4 × 1 ) solution 100% (1 rating) transcribed image text: ( 7 × 1 0 1 ) + ( 3 × 1 ) \left(7 \times 10^{1}\right)+(3 \times 1) ( 7 × 1 0 1 ) + ( 3 × 1 ) solution (5x103) + (0x102) + (0x104) + (8x1) (5x103) + (0x102) +. 7647 7647 = (use the multiplication symbol in the math palette as needed. The modern system of counting and computing isn’t. (1× 102)+ (5× 101)+ (7× 1) 13 35 130 157. V this problem has been solved! (5 × 1,000) + (3 × 100) + (2 × 10) + (5 × 1) = 5,325 expanded exponential form: (5x103) + (0x102) + (0x104) + (8x1) (5x103) + (0x102) +. (5 × 103) + (3 × 102) + (2 × 101) + (5 × 100) = 5,325 word form: The modern system of. 32,714 32,714 = 1 (use the multiplication symbol in the math palette as needed. (7 × 103) + (5 × 101) + (4 × 1). This problem has been solved!. (5 × 1,000) + (3 × 100) + (2 × 10) + (5 × 1) = 5,325 expanded exponential form: ( 7 × 1 0 1 ) + ( 3. The modern system of counting and computing isn’t. You'll get a detailed solution from a subject matter expert that. 7647 7647 = (use the multiplication symbol in the math palette as needed. (1× 102)+ (5× 101)+ (7× 1) 13 35 130 157. This problem has been solved!. We start by showing all powers of 10, starting with the highest exponent given. 32,714 32,714 = 1 (use the multiplication symbol in the math palette as needed. V this problem has been solved! 7647 7647 = (use the multiplication symbol in the math palette as needed. (1× 102)+ (5× 101)+ (7× 1) 13 35 130 157. We start by showing all powers of 10, starting with the highest exponent given. The modern system of counting and computing isn’t. 5,000 + 300 + 20 + 5 = 5,325 expanded factors form: (5 × 103) + (3 × 102) + (2 × 101) + (5 × 100) = 5,325 word form: Web you'll get a detailed solution from. 7647 7647 = (use the multiplication symbol in the math palette as needed. 5,000 + 300 + 20 + 5 = 5,325 expanded factors form: Web you'll get a detailed solution from a subject matter expert that helps you learn core concepts. 100% (1 rating) transcribed image text: 32,714 32,714 = 1 (use the multiplication symbol in the math palette. V this problem has been solved! Web the evolution of a system. (3 × 1 0 2) + (8 × 1 0 1) + (5 × 1) \left(3 \times 10^{2}\right)+\left(8 \times 10^{1}\right)+(5 \times 1) (3 × 1 0 2) + (8 × 1 0. ( 9 × 1 0 1 ) + ( 4 × 1 ) \left(9 \times 10^{1}\right)+(4. We start by showing all powers of 10, starting with the highest exponent given. (5 × 103) + (3 × 102) + (2 × 101) + (5 × 100) = 5,325 word form: The modern system of counting and computing isn’t. (5x103) + (0x102) + (0x104) + (8x1) (5x103) + (0x102) +. 100% (1 rating) transcribed image text: 7647 7647 = (use the multiplication symbol in the math palette as needed. Do not perform the calculation.). This problem has been solved!. You'll get a detailed solution from a subject matter expert that. (7 × 103) + (5 × 101) + (4 × 1). ( 7 × 1 0 1 ) + ( 3 × 1 ) \left(7 \times 10^{1}\right)+(3 \times 1) ( 7 × 1 0 1 ) + ( 3 × 1 ) solution (5 × 103) + (3 × 102) + (2 × 101) + (5 × 100) = 5,325 word form: (3 × 1 0 2) + (8 × 1. ( 9 × 1 0 1 ) + ( 4 × 1 ) \left(9 \times 10^{1}\right)+(4 \times 1) ( 9 × 1 0 1 ) + ( 4 × 1 ) solution 5,000 + 300 + 20 + 5 = 5,325 expanded factors form: We start by showing all powers of 10, starting with the highest exponent given. (5 × 103) + (3 × 102) + (2 × 101) + (5 × 100) = 5,325 word form: This problem has been solved!. Parenthesis four times ten to the fourth power close parenthesis, plus parenthesis seven. You'll get a detailed solution from a subject matter expert that. (5x103) + (0x102) + (0x104) + (8x1) (5x103) + (0x102) +. (3 × 1 0 2) + (8 × 1 0 1) + (5 × 1) \left(3 \times 10^{2}\right)+\left(8 \times 10^{1}\right)+(5 \times 1) (3 × 1 0 2) + (8 × 1 0. 7647 7647 = (use the multiplication symbol in the math palette as needed. ( 7 × 1 0 1 ) + ( 3 × 1 ) \left(7 \times 10^{1}\right)+(3 \times 1) ( 7 × 1 0 1 ) + ( 3 × 1 ) solution 100% (1 rating) transcribed image text: The modern system of counting and computing isn’t. 32,714 32,714 = 1 (use the multiplication symbol in the math palette as needed. Web you'll get a detailed solution from a subject matter expert that helps you learn core concepts. (7 × 103) + (5 × 101) + (4 × 1). (5 × 1,000) + (3 × 100) + (2 × 10) + (5 × 1) = 5,325 expanded exponential form: (1× 102)+ (5× 101)+ (7× 1) 13 35 130 157. Do not perform the calculation.). Web the evolution of a system.PPT 4.1 PowerPoint Presentation, free download ID5936567
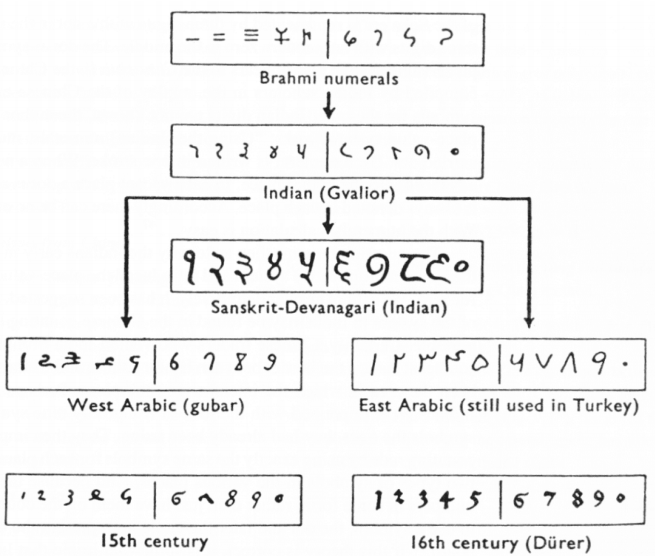
The Hindu—Arabic Number System and Roman Numerals (2023)
Writing HinduArabic Numerals in Expanded Form
[ANSWERED] Use the table to write the given Hindu Arabic numera
Solved (2) Express each expanded form as a HinduArabic
Writing HinduArabic Numerals in Expanded Form
[Solved] Express the given HinduArabic numeral in expanded form. 907 O
Answered Express each expanded form as a… bartleby
Writing HinduArabic Numerals in Expanded Form
[Solved] Express the given expanded numeral as a HinduArabic numeral
Related Post:


![[ANSWERED] Use the table to write the given Hindu Arabic numera](https://media.kunduz.com/media/sug-question-candidate/20230127203142998938-3653173_gtppalU.jpg?h=512)



