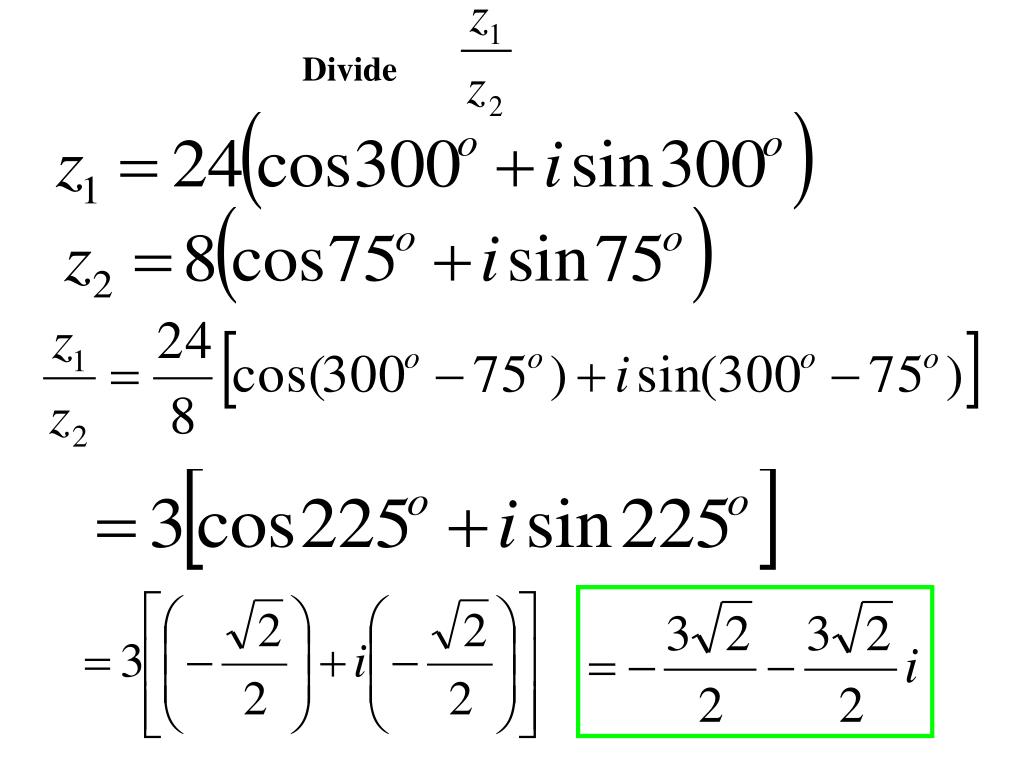Express The Complex Number In Trigonometric Form
Express The Complex Number In Trigonometric Form - Converting to polar from rectangular, x = 5 and y. 1 − i this problem has been solved! Z = r(cos θ + i sin θ), where r = |a + bi| is the modulus of z, and tan θ = b. ∙ xr = √x2 + y2. Web complex number in trigonometric form. ⇒ r = √12 + ( −√3)2. To convert to trigonometric form. As such, it is really useful for adding and subtracting complex numbers. Z = a+ bi = |z|(cos(θ)+isin(θ)) z = a + b i = | z. The number's real part and the number's imaginary part multiplied by i. Z = a+ bi = |z|(cos(θ)+isin(θ)) z = a + b i = | z. 1 − i this problem has been solved! Express the angle θ in radians where 0 is equal to or lesser than. Web complex number in trigonometric form. Web 6 = 6 ⋅ (cos 0o + isin 0o) see explanation. Web the rectangular form of a complex number is a sum of two terms: Web complex number in trigonometric form. Converting to polar from rectangular, x = 5 and y. The complex number z = a + b i can be written in trigonometric form: \(1−\sqrt{3}i\) to convert the following complex number from rectangular form to trigonometric polar. Express the angle θ in radians where 0 is equal to or lesser than. Z = r(cos θ + i sin θ), where r = |a + bi| is the modulus of z, and tan θ = b. Represent the complex number 5 + 7 i graphically and express it in its polar form. Write the complex number z=2+4i in. The complex number z = a + b i can be written in trigonometric form: Represent the complex number 5 + 7 i graphically and express it in its polar form. Express the angle θ in radians where 0 is equal to or lesser than. We can also plot a complex number given in. Determine the nth roots of complex. Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Use demoivre’s theorem to ind powers of complex numbers. Web trigonometric form of a complex number: Here x = 1 and y = − √3. Next, we must determine the argument. Next, we must determine the argument θ. Use demoivre’s theorem to ind powers of complex numbers. Precalculus complex numbers in trigonometric form trigonometric form of. Your number, which is in trigonometric form, can be expressed. The number 6 lies on a positive part of real axis, so the angle is 0 and the module is 6, so the trigonometric form. The number 6 lies on a positive part of real axis, so the angle is 0 and the module is 6, so the trigonometric form of 6 is:. Converting to polar from rectangular, x = 5 and y. Web the cis form of the answer is just another way to write it ( cis(θ) is a symbol that is, by. Web 6 = 6 ⋅ (cos 0o + isin 0o) see explanation. The number 6 lies on a positive part of real axis, so the angle is 0 and the module is 6, so the trigonometric form of 6 is:. Web the trigonometric form of a complex number z = a + bi is = r(cos i sin ); ⇒. Given a complex number in rectangular form expressed as z. Express the angle θ in radians where 0 is equal to or lesser than. ∙ xr = √x2 + y2. Web trigonometric form of a complex number: Web how do you express the complex number in trigonometric form: Precalculus complex numbers in trigonometric form trigonometric form of. ∙ xθ = tan−1( y x)x −π < θ ≤ π. Web the cis form of the answer is just another way to write it ( cis(θ) is a symbol that is, by definition, equal to cos(θ) + isin(θ) ). 1 − i this problem has been solved! As such, it. Represent the complex number 5 + 7 i graphically and express it in its polar form. Web the cis form of the answer is just another way to write it ( cis(θ) is a symbol that is, by definition, equal to cos(θ) + isin(θ) ). That is r(cosθ +isinθ) where. Given a complex number, z = a + b i, we first compute the modulus, r = a 2 + b 2. ⇒ r = √12 + ( −√3)2. How do you express the complex number in trigonometric form: Z = r ( cos θ + i sin θ), where a = r cos θ, b = r sin θ, r = a. To convert to trigonometric form. Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. As such, it is really useful for adding and subtracting complex numbers. Web how do you express the complex number in trigonometric form: Here x = 1 and y = − √3. The number 6 lies on a positive part of real axis, so the angle is 0 and the module is 6, so the trigonometric form of 6 is:. = b is called the argument of z. \(1−\sqrt{3}i\) to convert the following complex number from rectangular form to trigonometric polar. Given a complex number in rectangular form expressed as z. Web 6 = 6 ⋅ (cos 0o + isin 0o) see explanation. The complex number z = a + b i can be written in trigonometric form: Web how do you express the complex number in trigonometric form: Write the complex number z=2+4i in trigonemetric form.PPT Trigonometric Form of a Complex Number PowerPoint Presentation
Solved Express the complex number in trigonometric form 2 +
Find the product of the complex numbers. Express your answer in
Trigonometric Form Into A Complex Number
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
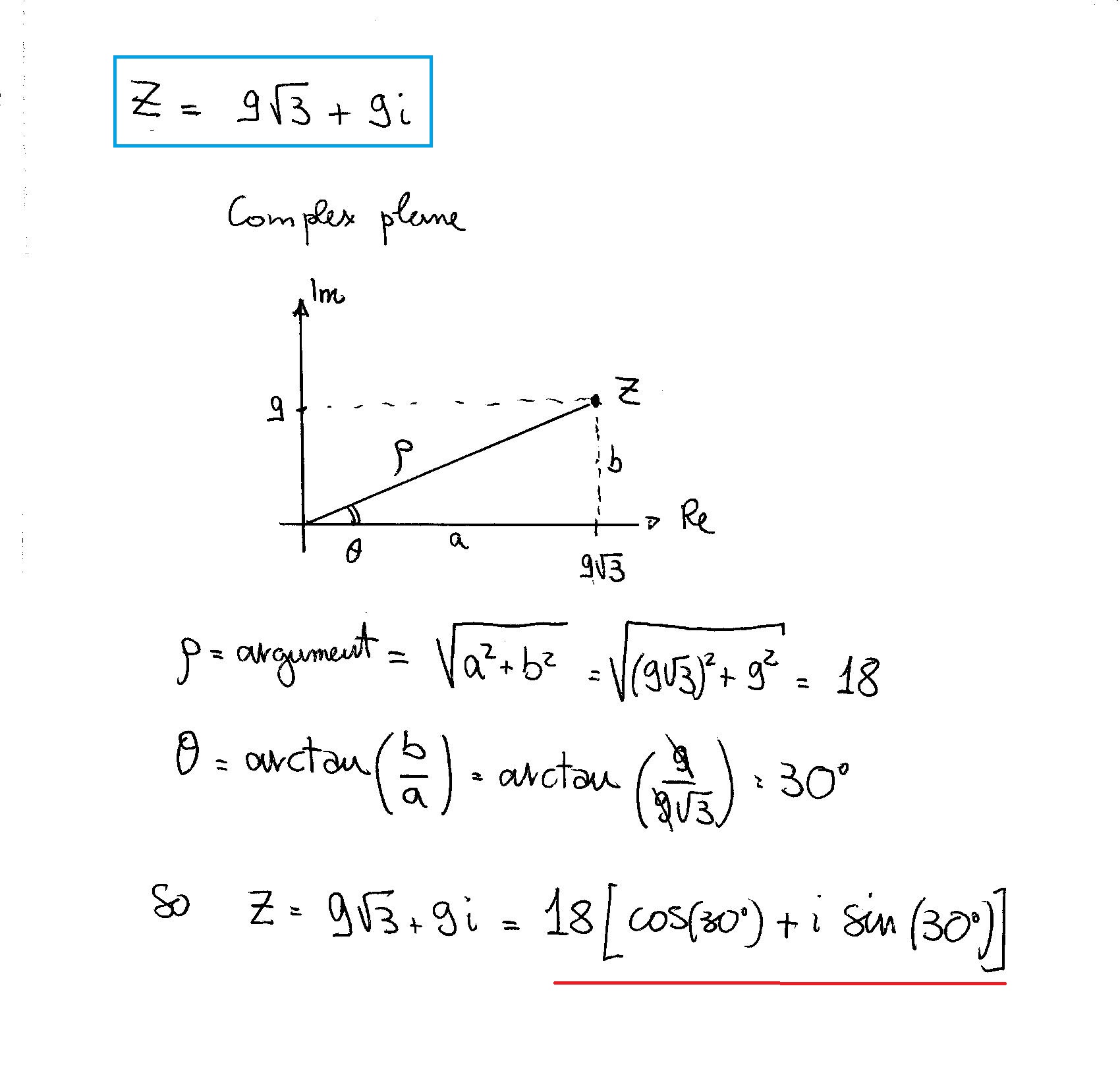
How do you express the complex number in trigonometric form 9(sqrt3
PPT 6.5 Trig. Form of a Complex Number PowerPoint Presentation, free
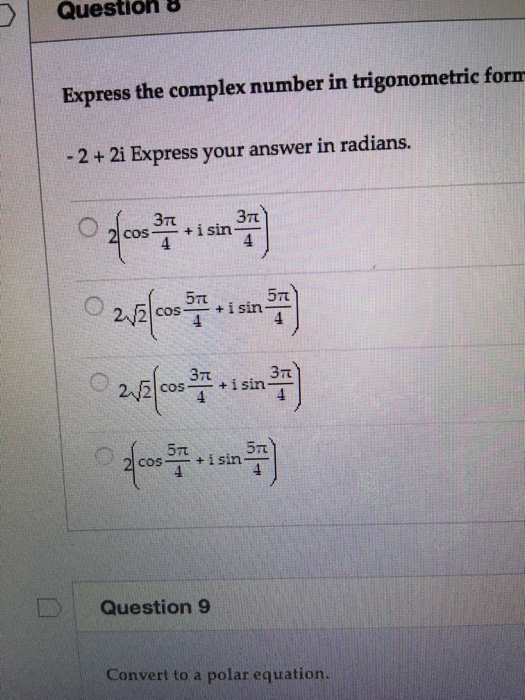
Express the complex number in trigonometric form. 2 2i
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
PPT Trigonometric Form of Complex Numbers PowerPoint Presentation
Related Post: